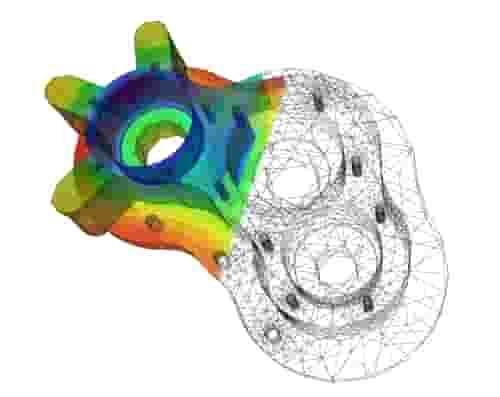
有限元分析是用较简单的问题代替复杂问题后再求解。它将求解域看成是由许多称为有限元的小的互连子域组成,对每一单元假定一个合适的(较简单的)近似解,然后推导求解这个域总的满足条件(如结构的平衡条件),从而得到问题的解。这个解不是准确解,而是近似解,因为实际问题被较简单的问题所代替。由于大多数实际问题难以得到准确解,而有限元不仅计算精度高,而且能适应各种复杂形状,因而成为行之有效的工程分析手段。
有限元是那些集合在一起能够表示实际连续域的离散单元。有限元的概念早在几个世纪前就已产生并得到了应用,例如用多边形(有限个直线单元)逼近圆来求得圆的周长,但作为一种方法而被提出,则是最近的事。有限元法最初被称为矩阵近似方法,应用于航空器的结构强度计算,并由于其方便性、实用性和有效性而引起从事力学研究的科学家的浓厚兴趣。经过短短数十年的努力,随着计算机技术的快速发展和普及,有限元方法迅速从结构工程强度分析计算扩展到几乎所有的科学技术领域,成为一种丰富多彩、应用广泛并且实用高效的数值分析方法。
APPLICABLE INDUSTRY
SUITABLE PRODUCT
CASE